Introduction to Relational Algebra

by K. Yue

1. Introduction

• More theoretical query languages of the relational model:
  • relational algebra
  • relational calculus.
• Relational algebra:
  • include a set of basic and derived set-theoretic operations.
  • procedural: specify a sequence of operations.
  • Operations can be unary or binary.
  • Results are also a relation: closure property => chained operations.

2. Basic Operations

Cartesian Product

• Same as the usual definition of Cartesian Product of two sets.
  • Remember that a relation is a set.
• Merge all possible information from two relations.
• Also called Cross Product or Cross Join.
• Name ambiguity may be resolved by using full names.
• The cardinality of a set S is |S|, the number of elements in the set.
• |RxS|= |R| * |S|
• Not very useful in practice as the result can be large and constructing the result can be time consuming.

Example:

R(A,B,C) has three tuples. S(A,D) has four tuples.

The result of R x S always has 12 tupes with the schema (R.A, B, C, S.A, D).

Select

• Unary operation.
• Select tuples (with the same schema) based on a Boolean condition.
• Conditions may includes attributes in the relational schema.
• 'Horizontal' subset.
• Not to be confused with the Select statement in SQL.

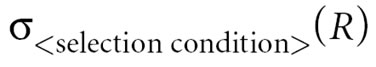
σcond(R) = {t | t ε R and cond}

Project

• Unary opera to in
• Select attributes from tuples.
• Duplicate results removed (because a relation is a set).
• 'Vertical' subset.

πc1, .., cm(R) = {s | there exists t ε R (t(ci) = s(ci), for 1 <= i <= m)}

Union

• The set union operator.
• Condition for R U S: R and S must be union compatible. Their relation schema must have compatible schema with the same structures.

R U S = {t | t ε R or t ε S}

Example:

Suppose StaffID and FacultyID are uniion compatible.

 πStaffID(Staff) U πFacultyID(Faculty)

Difference (Minus)

• The set difference operator.
• R - S: R and S must be union compatible.

R - S = {t | t ε R and not (t ε S)}

Rename

• Rename the names of selected attributes in a relation.
• Maybe used to rename attributes before a set operation.

• The basic set of operations is complete. Other relational algebra operations can be derived from them.

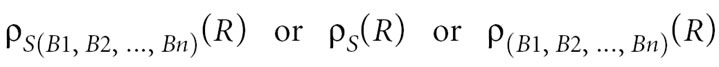
3. Common Derived Operations

Theta-join

• Allow the application of condition on Cartesian product.
• There are still redundant data on common attributes.
• Allow the query engine to throw away tuples not in the result immediately.
• Conceptually, a Cartesian Product followed by a selection.
• Not usually used.

R1 |x|Θ R2

Equi-join

• Theta-join where the condition involves only equality comparisons.
• There are still redundant data on common attributes.
• Not usually used.

Natural Join

• Remove redundant common attributes.
  • Equi-join.
  • Projection to remove redundant common attributes.
• Used very frequently to combine two tables.
• If two relations do not share any common attributes, their natural join is the same as their Cartesian Product.

Let C1, C2, ... Cm be the common attributes of R1 and R2.

R |x| S = πA1, A2, .. Al(σR.C1=S.C1,.., R.Cm=S.Cm(RxS)

where A1, A2, ... Al is the list of components in RxS except S.C1, S.C2,.. S.Cm.

Example:

The schema of R(A,B) |x| S(A,C) is ABC. The schema of R(A,B) x S(A,C) is {R.A, B, S.A, C}.

Exercise

Let the cardinality of R(A,B) be 5 and the cardinality of S(A,C) be 6. What is the range of the cardinality of R(A,B) |x| S(A,C)?

Other Joins

• Some other joins are outer join, inner join and semi-join.
• They can be defined through relational algebra expressions based on the basic operations.
• Look them up when needs arise.

Division

• R / S
• Condition: the domain of S is a proper subset of R.
• Let the schemes of R, S and T be dom(R), dom(S) and dom(T) = dom(R) - dom(S) respectively.
• R / S = {t | t in dom(T) and for all s ε S, there exist r ε R such that r = st}.

Example:

Consider:

Supplier(SNum,  SName,  SCity,  Status)
Part(PNum, PName,  Color,  Weight)
Supply(SNum,  PNum, Quantity)

An example of relation instance:

Supplier:

Part:

Supply:

π SNUM (SUPPLIER):

π SNUM (SUPPLY):

σ STATUS >= 10 (SUPPLIER):

(π SNUM (SUPPLIER)) * (σ STATUS >= 10 (SUPPLIER)):

(π SNUM (SUPPLIER)) |X| (σ STATUS >= 10 (SUPPLIER)):

π SNUM, PNUM (SUPPLY)):

π PNUM (σ COLOR = ‘Green’ (PART)):

π SNUM, PNUM (SUPPLY)) / π PNUM (σ COLOR = ‘Green’ (PART)):

Exercise:

Work on some of the query questions listed in the Supply database example.

4. Epilog

Some shortcomings of Relational Algebra:

• Cannot navigate tuples.
  • e.g. Show the available total quantities of all parts.
• Cannot deal with recursion.
  • e.g. for the relation Employee(SS#, Supervisor_SS#, ...), find all supervisors (direct or indirect).
  • May extend to logical database, e.g. Datalog.