Introduction to Functional Dependency and Normalization

by K. Yue

1. Introduction to Normalization

• Normal forms (NF): a set of rules to detect poor database design so they can possibly be improved by decompositions.
• Require the concepts of various kinds of data dependency: constraints or restrictions between two sets of attributes.
  1. Functional dependency (FD, most important: used to define NF, up to BCNF)
  2. Multi-valued dependency (MVD for defining 4NF)
  3. Join dependency (JD for defining 5NF)
• Some common normal forms in ascending order: 1NF, 2NF, 3NF, BCNF, 4NF, 5NF, DKNF, 6NF.
• Higher normal forms are more restrictive and signify better designs.
• A relation in a higher normal form implies that it is in a lower normal form, but not vice versa.

Example

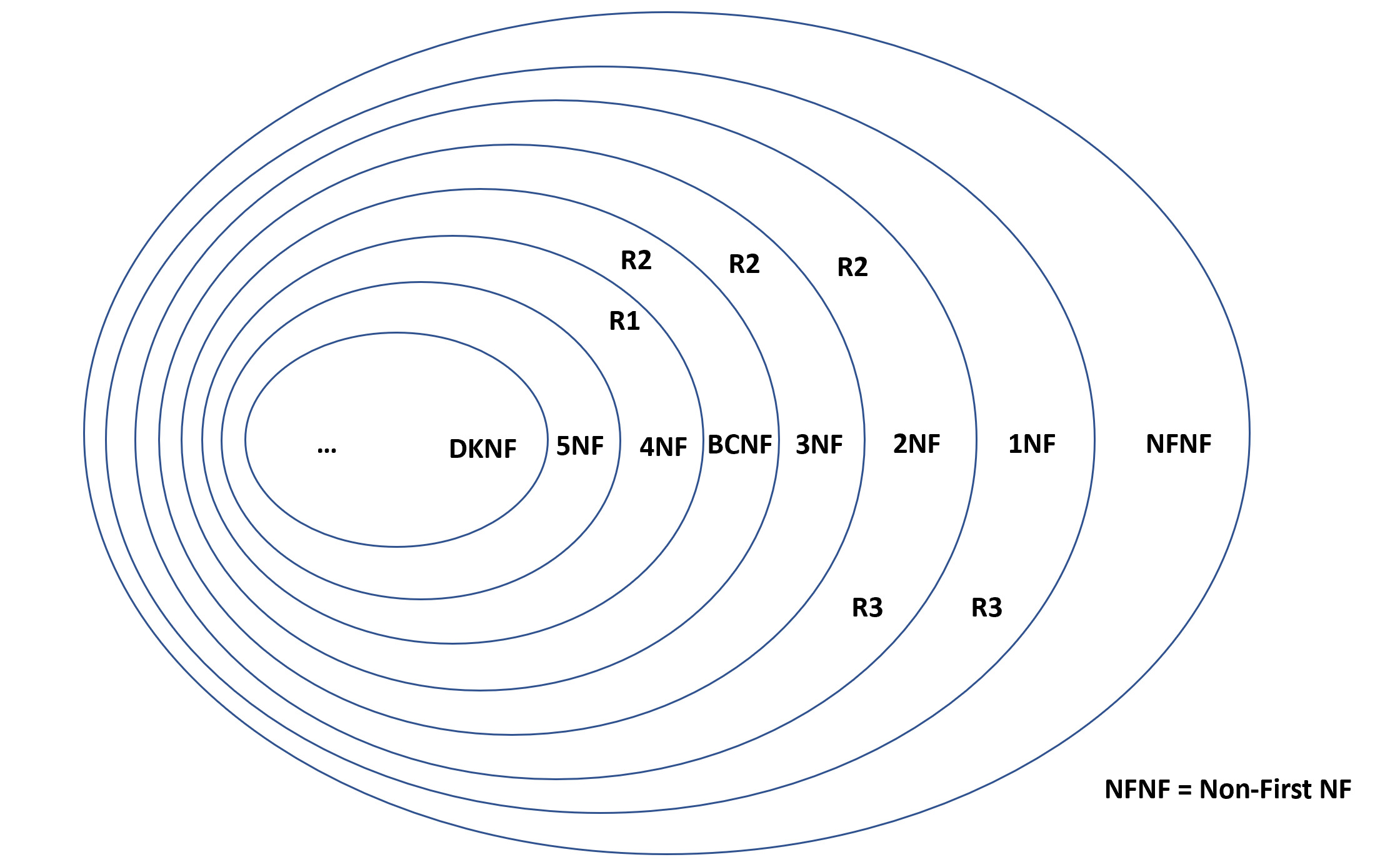
If a relation R1 is in 4NF, then R1 is also in BCNF, 3NF, 2NF and 1NF. Refer to the diagram below for R1, R2, and R3. NFNF stands for Non-First Normal Form.

If a relation R2 is in 2NF, then

1. It is in 1NF,
2. it may or may not be in 3NF, and
3. it may or may not be in BCNF.

If a relation R3 is not in 3NF, then

1. It is not in BCNF.
2. It may or may not be in 1NF or 2NF.

The relations R1 and R3 in this example are depicted in the Venn's Diagram:

1.1 General Overview

• In general, the higher the normal form a relation is in, the better the logical design of the relation (in terms of avoiding redundancy and inconsistency).
• However, it may be necessary to consider other issues, especially performance.
  1. Higher normal forms may be achieved by decompositions, resulting in more relations.
  2. More joins may then be needed to provide the data for a query, decreasing performance.
• 1NF is usually assumed. However, there are relations not in 1NF in both theory and practice.
  • For example, a composite data type may be supported by a specific DBMS vendor. E.g., JSON, XML, GeoCode, etc.
• 2NF is more interesting for historical reasons.
• 4NF or above involves data dependency that is hard to understand and use. They are usually not used in practice.
• Based on the concept of functional dependencies (FD), the most important normal forms are
  1. 3NF and
  2. BCNF (Boyce-Codd Normal Form).

2. Functional Dependencies (FD)

• Each attribute in a database represents certain data information in the application.
• There can be dependency between data.
• For example, types of dependency and relationship between two sets of attributes can be:
  • Many to one (0..* to 0..1): Functional Dependency (FD)
  • Many to many (0..* to 0..*): Multi-Valued Dependency (MVD)
• These relationships are the results of assumptions we made about the application requirements.

Example:

A student, {StudentId: 1233457} can be associated with only one GPA: {GPA: 3.00}
However, several students can have the same GPA: {GPA: 3.00}

StudentId -> GPA    (FD)
(many)         (one)

On the other hand, a student {StudentId: 1233457} can take many courses: {cid: CSCI4333}, {cid:CSCI 2315}, {cid: CSCI3331},...
Many students can take the same course: {StudentId: 1233457}, {StudentId: 2233490}, {StudentId: 3333457},... take {cid: CSCI4333}.

Under these assumptions

StudentId ->-> cid    (MVD: not covered in this course)
(many)            (many)

2.1 Many to one relationships

Example

For many applications, the relationship between SSN and FName are many to one in a relation R(..,SSN, FName, ...)

SSN        ->     FName
(many)                 (one)

Assumptions:

1. A SSN uniquely identifies a person.
2. Given a SSN, there can only be one first name associated with it (not allowing/storing alias, etc.)
3. Many different SSN's (persons) may have the same first name.
4. There should not be two tuples with the same SSN, but different FName in all instances of R.

Terms:

1. SSN uniquely determines FName.
2. FName is functionally determined by SSN.
3. There is a functional dependency SSN -> FName.
4. Hence, a functional dependency specifies a many to one relationship between two sets of attributes.

For example, consider the relation instance:

The relation instance is not allowed if we assume SSN -> FName.

Example

In a university, there may be a many-to-one relationship between {CourseId, StudentId} and {Grade}.

Interpretations:

1. A student may have only one grade for a course.
2. We say that there is a FD:
   • CourseId, StudentId -> GRADE, or
   • {CourseId, StudentId} determines Grade.
3. Note that under a different set of assumptions, the functional dependency may not be true.
4. For example, if a student is allowed to retake a course, then he may have two grades for the same course (in different semesters), then CourseId, StudentId -> Grade is false.
5. We may instead have {CourseId, StudentId, Semester, Year}-> {Grade}

• Hence, a functional dependency is a result of the requirements and business logics of the applications. 
• There is no universally true non-trivial functional dependency.
• In other words, FD depend on the semantics of the problem.

Note that AB->CD is a shorthand notation for {A,B} -> {C,D}

FD such as AB-> A, AB->B, AB->AB, A->A are trivial. They are always mathematically true, but do not capture any data requirements.

Example:

In most applications, we have

SSN -> FName             (i.e.  a person has only one SSN.)

However, in a criminal database, several bad guys may use the same fake SSN, and thus

SSN -> FName  may not be true.

Or, if you are dealing with an international database with many countries, each country may has its own SSN.  Two countries may issue the same SSN.  Hence,

SSN -> FName   is not true.

We may instead have  SSN, CountryId -> Name.

2.2 Definition of FD

• A relation schema R is said to satisfy the functional dependency X -> Y if for any relation instance r that uses R, if there exists two tuples s and t ∈ r such that s[X] = t[X], then s[Y] = t[Y].
  1. (∃s, t ∈ r) (s[X] = t[X]) => s[Y] = t[Y]
  2. i.e.  same value in X implies same value in Y.

Example:

This instance r1 of R violates X->Z.

This instance r2 of R does not violate X->Y.

However, this instance r2 does not prove that X->Y.

In order to have X-> Y, all instances r of R must not violate the condition.

Examples:

DeptId -> ManagerId:

There are no two tuples with the same DeptId but different ManagerId.  Meaning: a department can have only one manager.

CourseId, StudentId, Semester -> Grade

There are no two tuples with the same CourseId, StudentId and Semester, but different Grade.  Meaning: any student taking a course in a semester has an unique grade. Note that it may not be true for a different university. Instead, the following may be true:

CourseId, StudentId, Year, Semester -> Grade

Example

Consider the following relation:

Supply(SupplierId, SupplierName, ProductId, ProductDesc, Quantity, ArrivalTime)

The relation stores the quantities and arrival times of shipments of products (identified by ProductId) from suppliers (Identified by SupplierId). A supplier may not have a unique name. Furthermore, the product description, ProductDesc, may be the same for two products. A supplier may supply the same product many times, each with a different ArrivalTime.

The functional dependencies (FD) of the relation may be:

SupplierId -> SupplierName
ProductId -> ProductDesc
SuplierId, ProductId, ArrivalTime -> Quantity

Decomposition:

Supplier(SupplierId, SupplierName) {SupplierId -> SupplierName}
Product(ProductId, ProductDesc) {ProductId -> ProductDesc}
Supply(SuplierId, ProductId, ArrivalTime, Quantity) {SuplierId, ProductId, ArrivalTime -> Quantity}

Example (from Spring 2019 HW):

Consider the following relation GO:

GO(GroupId, GroupName, GroupEMail, GroupChairId, GroupChairLName, GroupChairFName, GroupMemberId, GroupMemberMajor)
The relation stores information about student groups, their chair persons and members. Chair persons and members are students with unique student ids (stored as values in GroupChairId and GroupChairLName respectively). GroupId uniquely identifies a group, and a group has a unique name, and an email address (that may not be unique.) For example, three tuples are shown below.

Bryan Lee is the chair student of the group G1 Biology. The first three tuples also store information of three members of group G1

(a) List all applicable functional dependencies. (Make reasonable assumptions if necessary.)

GroupId -> GroupName, GroupEMail, GroupChairId
GroupName -> GroupId
GroupChairId -> GroupChairLName, GroupChairFName
MemberId -> GroupMemberMajor

Assumptions:

1. A group has a unique chairperson.
2. A student may be a chairperson or a member for multiple groups.
3. A student has a unique major (e.g., no double majors).

(b) What are the candidate keys?

{GroupId, MemberId} and {GroupName, MemberId}

(c) What is the highest normal form? Why?

1NF. For example, GroupId -> GroupEMail violates 2NF.

(d) If the highest normal form is not BCNF, can you decompose the relation GD losslessly into component relations in BCNF while preserving functional dependencies? If yes, how. If no, why?

1. Group(GroupId, GroupName, GroupEMail, GroupChairId) {GroupChairId references Student(StudentId)}
2. Membership(GroupId, MemberId) {MemberId references Student(StudentId)}
3. Student(StudentId, StudentLName, StudentFName, Major, …)

Note that changes of attribute names in the member tables. For example, StudentLName is more appropriate than ChairLName since a student may not be a chair.